Quantum vs. Classical - Data Management Computational Complexity

In the ever-evolving landscape of data management, the distinction between quantum and classical computing is becoming increasingly significant. Traditional methods of searching and processing vast amounts of data are being challenged by the advent of quantum algorithms, which promise to drastically improve efficiency and performance. Among these quantum innovations, Grover’s Algorithm stands out as a revolutionary development in the field of quantum search efficiency.

This post delves into the complex world of computational complexity in data management, comparing and contrasting classical approaches with their quantum counterparts. As we explore the mechanics and implications of Grover’s Algorithm, we will uncover how quantum computing is not just a theoretical exercise but a practical tool poised to transform the data management industry. Read through with me, as we navigate through the intricate details of these computing paradigms and their potential to reshape our understanding and handling of data in an increasingly digital world.

Traditional Data Platforms: Foundations

In traditional data platforms, core database operations exhibit the following ‘common’ complexities:

• Searching: Unsorted data typically requires linear search algorithms with complexity O(n), where n is the size of the dataset. Sorted datasets can use binary search, achieving O(log n). However, more advanced indexing structures like B-trees further reduce this complexity.

• Insertion/Deletion: These operations, especially in sorted environments, tend to have O(n) complexity as data may need to be shifted. Balanced trees can reduce this to O(log n).

• Complex Queries and Joins: The complexity of these operations depends on the algorithms used and data structures. Nested-loop joins can reach O(n²), while optimized hash joins or merge joins can be closer to O(n log n) or even O(n) with suitable structures.

Quantum Data Management: A New Paradigm

Quantum Data Management Platforms introduce groundbreaking algorithms with potentially significant advantages:

• Grover’s Search Algorithm: This quantum algorithm offers a quadratic speedup for unsorted searches. Instead of O(n) for a linear search, the complexity becomes approximately O(√n).
• Quantum Amplitude Amplification: A generalization of Grover’s algorithm, this extends the quadratic speedup potential to a wider range of computational problems beyond pure searching.
• Quantum-Inspired Indexing: Research into the adaptation of traditional indexing structures like B-trees and hash tables to the quantum domain is ongoing. These may lead to further logarithmic-like improvements in specific query scenarios.

Key Considerations and Caveats

It’s crucial to highlight several points:

• Quantum Error Correction: Real-world QDMPs will require extensive error correction, introducing overheads that impact overall computational complexity. The extent of this overhead will depend on the progress in developing robust quantum computers.
• Problem-Specific Suitability: Quantum algorithms are highly specialized. Grover’s search, for instance, is excellent for unstructured search problems but offers less advantage when data possesses some internal structure.
• Algorithm Development: The field of quantum database algorithms is still in its infancy. The full potential of QDMPs relies on the continual development of novel algorithms that exploit quantum phenomena.

Mathematical Example: Search Complexity

Let’s illustrate with a concrete example — searching for a specific item in a database:

• Traditional (linear search): Complexity — O(n)
• Quantum (Grover’s algorithm): Complexity — O(√n)

If our database has a billion entries (n = 1,000,000,000), a traditional search might take a billion steps on average. Grover’s algorithm could potentially find the item in roughly 30,000 steps — a dramatic difference.

Let’s break down how Grover’s algorithm achieves this impressive search efficiency. It’s important to note that Grover’s algorithm, at its heart, doesn’t directly search a database in the traditional sense; it instead solves the following kind of problem:

Problem: You have a function (often called an ‘oracle’) that takes an input and outputs ‘1’ if the input is your desired solution and ‘0’ otherwise. Your goal is to find an input that makes the function produce a ‘1’.

Grover’s Algorithm Intuition

Here’s the core idea behind Grover’s algorithm, presented in a simplified way:

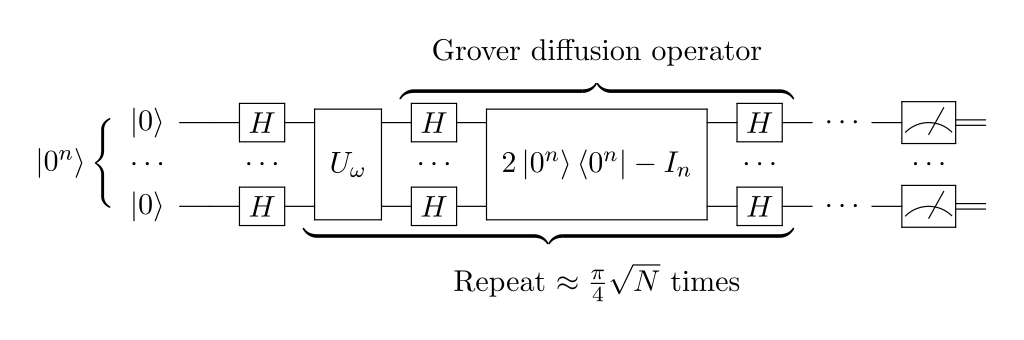
Step 1. Superposition: Instead of examining database entries one at a time, Grover’s leverages quantum superposition. The algorithm puts a quantum system into a superposition representing all possible database entries equally.

Step 2. Oracle Marking: The oracle function is applied in a quantum way, causing it to ‘mark’ the correct entry by negating its amplitude (think of flipping its sign).

Step 3. Amplitude Amplification: The key step — Grover’s algorithm uses an operation called ‘diffusion’ to amplify the amplitude of the marked entry. Intuitively, this makes it “stand out” from the crowd of other entries.

Step 4. Iteration: Steps 2 and 3 are repeated multiple times. Each iteration amplifies the correct answer further.

Why So Fast?

Interference: The amplitude amplification step uses quantum interference to cleverly increase the probability of measuring the correct answer while simultaneously decreasing the probability of measuring incorrect ones. Success Probability: After a specific number of iterations (roughly the square root of the number of entries), the probability of measuring the correct solution becomes very high.

Analogy

Think of a lottery with a billion tickets, but only one winner. Normally, you’d check tickets one by one. Grover’s does something akin to:

1. Putting all the tickets in a quantum ‘box’ and shaking it.
2. Magically marking the winning ticket subtly.
3. Having a way to shake the ‘box’ so the winning ticket tends to float to the top.
4. Repeating step 3 a few times. Now when you open the box, you have a high chance of picking the winner.

Addressing Our Numbers

With a billion entries (n = 1,000,000,000), the square root of n is approximately 31,622. This roughly aligns with the 30,000 steps mentioned. Importantly, the number of steps in Grover’s algorithm doesn’t grow at the same rate as a traditional search.

Important Notes

• Oracle Creation: Adapting real-world problems into an oracle suitable for Grover’s search can be difficult.
• Limitations: Grover’s is best suited for unstructured searches. If data has a known structure, traditional methods might work better.

Unveiling the Math: Amplitude Amplification in Grover’s Algorithm

Grover’s algorithm’s power lies in its core operation — amplitude amplification. Let’s delve into the mathematical details of this critical step.

Setting the Stage: Hilbert Space and Notation

• We work in a Hilbert space representing the superposition of all possible database entries (n qubits). Each basis state represents one entry.
• Denote the initial uniform superposition as: |s⟩ = (|0⟩ + |1⟩)/√2 (for single qubit) or a similar equal superposition for n qubits.
• The oracle function is represented by a unitary operator, O, that flips the sign of the desired solution state while leaving others unchanged.

The Magic: Amplitude Amplification Operator

The key operator in Grover’s diffusion is the Grover operator, denoted as G. It’s constructed using the reflection operator, R:

R = 2|s⟩⟨s⟩ — I (where I is the identity operator)

The Grover operator, G, is then defined as:

G = R — (2|0⟩⟨0⟩ + 2|1⟩⟨1⟩) = R — 2I

Understanding the Operators

• R reflects the current state around the uniform superposition

  s⟩.

• The additional term -2I ensures the overall reflection doesn’t change the norm (length) of the state vector.

The Amplification Process

Now comes the magic! We apply the oracle (O) followed by the Grover operator (G) in a loop:

|ψ⟩ = G * O |s⟩

This sequence (GO) cleverly amplifies the amplitude of the desired solution state while diminishing those of incorrect entries.

Iterative Amplification

Repeating the sequence (GO) multiple times enhances this amplification effect.

Mathematically, after t iterations:

|ψ_t⟩ = (GO)^t |s⟩

Finding the Optimal Number of Iterations

The number of iterations (t) for optimal amplification depends on the number of entries (n). Here’s the sweet spot:

t ≈ √(π * n / 4)

With this number of iterations, the probability of measuring the desired solution becomes very high.

Inner Workings: A Geometric View

Imagine the initial state as a vector in the n-dimensional Hilbert space. The oracle “marks” the solution by rotating it. Subsequent applications of the Grover operator act like further rotations, amplifying the solution’s projection onto the desired subspace while diminishing those of incorrect entries.

Complexity Analysis

The number of iterations (t) scales as the square root of n, a significant improvement over the linear search complexity (O(n)). This translates to the dramatic speedup observed in Grover’s algorithm.

Conclusion

By leveraging the power of quantum superposition, oracle marking, and the Grover operator’s clever manipulation of amplitudes, Grover’s algorithm achieves an exponential speedup for search problems in unstructured databases.

While implementing this in real-world quantum computers presents challenges, the theoretical foundation of amplitude amplification provides a fascinating glimpse into the potential of quantum algorithms.