This blog post proposes a novel concept - ETL-C, a context-first approach for building Data / AI platforms in the Generative AI dominant era. More discussions to follow.
Think of your data as a sprawling city.
Raw data is just buildings and streets, lacking the vibrant life that gives it purpose. ELT-C injects that vibrancy - the demographics, traffic patterns, and even the local buzz. With the added dimensions of Context Stores, your data city becomes a place of strategic insights and informed action.
As we develop an increasing number of generative AI applications powered by large language models (LLMs), contextual information about the organization’s in-house datasets becomes crucial. This contextual data equips our platforms to effectively and successfully deploy GenAI applications in real-world scenarios, ensuring they are relevant to specific business needs and tailored to the appropriate contexts.
Let’s explore how this integrated approach empowers data-driven decision-making.
Introducing ELT-C
Let’s recap the key ETL stages followed by the Contextualize:
-
Extract The “Extract” stage involves pulling data from its original sources. These could be databases, applications, flat files, cloud systems, or even IoT devices! The goal is to gather raw data in its various forms.
-
Load Once extracted, data is moved (“Loaded”) into a target system designed to handle large volumes. This is often a data warehouse, data lake, or a cloud-based storage solution. Here, the focus is on efficient transfer and storage, minimizing changes to the raw data.
-
Transform This stage is all about making data usable for analysis. Transformations could include:
- Cleaning and standardizing data (e.g., fixing inconsistencies, handling missing values)
- Merging datasets from different sources
- Calculations or aggregations (like calculating totals or averages)
-
Contextualize Contextualization is the heart of ELT-C, going beyond basic data processing and turning your information into a powerful analysis tool. It involves adding layers of information, including:
-
Metadata: Descriptive details about the data itself, such as where it originated, when it was collected, what data types are included, and any relevant quality indicators. This makes data easier to understand, catalog, and use.
-
External Data: Enriching your data by linking it to external sources. This might include:
- Customer demographics: Supplementing sales transactions with customer age, location, or income data for better segmentation.
- Market trends: Adding industry reports or competitor data to contextualize your company’s performance.
- Weather data: Correlating weather patterns with sales trends or energy consumption patterns to understand external drivers.
-
User Data: Augmenting data with insights about how users interact with your products, services, or website. This could include:
- Website behavior: Tracking user navigation paths to reveal buying intent or improve site design.
- App engagement: Analyzing in-app behavior to identify churn indicators or opportunities to boost retention.
- LLM engagement: Flowback LLM analytics data as in-house technical / business users and end-customers of your platform interact with other LLM applications. This could include insights on the types of queries, responses, and feedback generated within the LLM ecosystem.
-
Example: ELT-C for Next Best Offers - Turning Data into Personalized Credit Card Solutions
Let’s see how the combination of metadata, external data, and user data could all be leveraged by a retail bank to optimize next-best credit card offers, with a focus on how contextualization enhances traditional approaches:
-
Metadata
- Example: Detailed metadata on customer transactions, product descriptions, and marketing campaign data. This includes timestamps, source systems, data types, and quality scores, etc.
- How it helps: Ensures the bank uses up-to-date, reliable information and can trace any issues back to the origin.
- Contextualize for Better Analysis: Knowing the recency of data is key for some offers (e.g., targeting recent high spenders). Metadata on the origin of data could reveal if certain marketing campaigns outperform others based on the data source, leading to refined targeting strategies.
-
External Data
- Example:
- Customer demographics (age, income, location)
- Market trends in interest rates, competitor offers, economic indicators
- How it helps: Broad segmentation (e.g., higher income bracket might qualify for a premium card) and understanding general market conditions.
- Contextualize for Better Analysis:
- Localized economic data alongside customer demographics could reveal underserved areas where the bank can expand its card offerings.
- Sudden changes in economic forecasts or competitor actions might trigger proactive offers to solidify relationships with existing customers.
- Example:
-
User Data
-
Website behavior: Tracking user navigation paths to reveal buying intent or improve site design. Going beyond basic page views, contextualization could incorporate external economic data or user demographics to understand if browsing behavior is driven by necessity or changing financial priorities.
-
App engagement: Analyzing in-app behavior to identify churn indicators or opportunities to boost retention. Contextualize for Better Analysis: Adding LLM-derived sentiment analysis of user support queries within the app adds a new dimension to understanding pain points. This can reveal issues beyond technical bugs, potentially highlighting misaligned features or confusing user experience elements.
-
LLM engagement: Flowback LLM analytics data as in-house technical / business users and end-customers of your platform interact with other LLM applications. This could include insights on the types of queries, responses, and feedback generated within the LLM ecosystem. This is where ELT-C shines! LLM queries can be correlated with other user actions across systems. For instance, are users researching competitor offerings in the LLM, then browsing specific product pages on the bank’s site? This context highlights a customer considering alternatives and the need for urgent proactive engagement.
-
Context Bridge & Stores
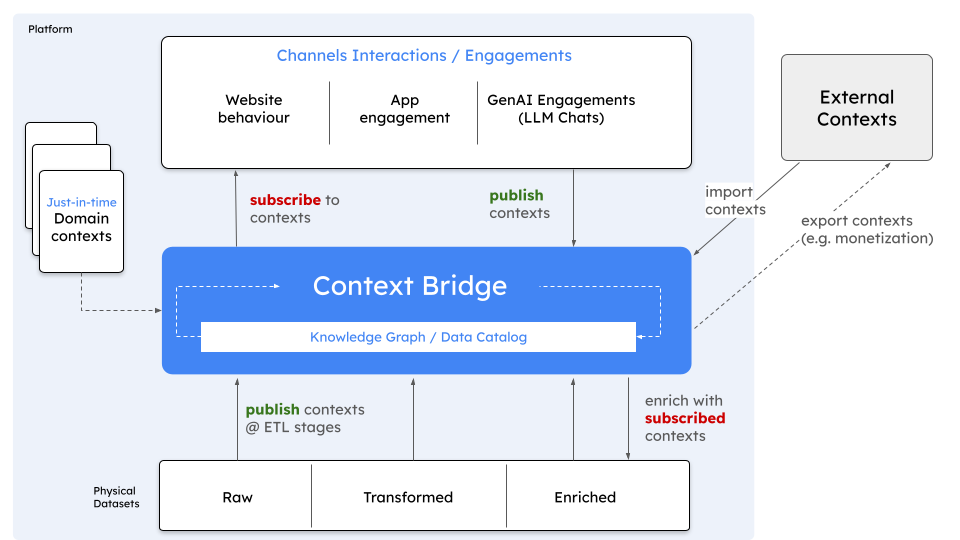
In image above, a Context Bridge that provides real time contexts across multiple publishers and subsribers. Context Stores can become even more powerful, when integrated with an Enterprise Knowledge Graph or Data Catalog (structured entity relationships meet flexible context stores for richer data analysis)
What is a Context Store?
A Context Store is a centralized repository designed specifically for storing, managing, and retrieving contextual data. It extends the concept of feature stores to encompass a broader range of contextual information that can power rich insights and highly adaptive systems.
How Context Stores Elevate Context Management:
- Centralization: Breaks down silos between isolated contextual data sources, creating a single source of truth for analytics and machine learning models.
- Accessibility: Democratizes access to contextual information, making it readily available to any relevant system or application.
- Governance: Implements consistent quality checks, security, and compliance management of context data.
- Real-time Insights: Enables systems to react rapidly to shifts in context, providing up-to-the-minute analysis and adaptive experiences.
Architecturally Significant Requirements (ASRs)
| No. | Requirement | Aspects |
|---|---|---|
| ASR1 | Data Storage and Management | - Accommodates diverse context types: metadata, user data, external data, embeddings. - Supports structured, semi-structured, and unstructured data formats. - Efficient storage and retrieval optimized for context search and analysis. |
| ASR2 | Real-time updates | - Integrates with streaming data sources for capturing dynamic changes in context - Updates contextual data with low latency for real-time use cases |
| ASR3 | Version Control | - Tracks historical changes to contextual data - Supports debugging and analysis of time-dependent insights and model behavior |
| ASR4 | Data Access and Retrieval | - Intuitive interface or query language for context discovery and exploration. - Supports queries for specific contextual information (by source, entities, timeframe) |
| ASR5 | Scalability and Performance | - Handles large volumes of contextual data without degradation. - Provides fast responses to search queries and data access requests. - Scales well to accommodate increasing data loads or user traffic. |
| ASR6 | Availability and Reliability | - Highly available to ensure continuous operation for context-dependent systems. - Incorporates fault tolerance and data replication to prevent data loss. |
| ASR7 | Security and Compliance | - Implements robust access controls and data encryption. - Adheres to relevant data privacy regulations (e.g., GDPR, CCPA). - Maintains audit trails for tracking data access and modifications. |
| ASR8 | Maintainability and Extensibility | - Offers straightforward administration features for data updates or schema changes. - Can be easily extended to support new context types or integrate with evolving systems. |
Context Stores vs Vector Stores
Data isn’t just about numbers and values. Context adds the crucial “why” and “how” behind data points. Context stores have the potential to handle this richness, while vector stores specialize in representing relationships within data.
Let’s delve into these specialized tools.
Similarities
- Purpose: Both context stores and vector stores aim to enhance how information is stored, retrieved, and utilized for analytics and machine learning models.
- Centralization: Both act as centralized repositories for their specific data types, improving accessibility and organization.
- Specialization: Both are specialized databases, unlike traditional relational databases, optimized for their unique data types (contextual features vs. embeddings).
Key Differences
| Feature | Context Store | Vector Store |
|---|---|---|
| Focus | Broad range of contxtual data | Numerical representations of data (embeddings) |
| Data Types | Metadata, structured data, text, external data, embeddings | Primarily numerical vectors (embeddings) |
| Search Methods | Metadata-based, text-based, feature searches | Similarity-based search using vector distances |
| Primary Use Case | Powering analytics, ML models with rick context | Recommendations, semantic search, similarity analysis |
How They Can Work Together
Context stores and vector stores are often complementary in modern data architectures:
-
Embedding Storage: Context stores can house embeddings alongside other contextual data, enabling a holistic view for machine learning models.
-
Semantic Search: Vector stores enhance how context stores access information, allowing searches for contextually similar items based on their embeddings.
-
Enriching ML Features: Context stores provide a variety of data sources to inform the creation of powerful features for ML models. These features might then be transformed into embeddings and stored in the vector store.
Context Stores and Knowledge Graphs (KGs)
Knowledge Graphs (KGs) and Context Stores can complement each other to significantly enhance how data is managed and utilized:
Synergy Between Knowledge Graphs and Context Stores
- Shared Goal: Both aim to enrich data with meaning and context, empowering more insightful analytics and fostering a deeper understanding of information.
- Complementary Strengths: KGs excel at capturing relationships between entities in a structured way, while context stores manage diverse contextual data beyond pre-defined relationships.
How They Can Work Together
-
Contextualizing Knowledge Graphs: Context stores can provide KG entities with richer context. Imagine a KG entity for a “product”.
A context store might house information about a specific product launch event, user reviews mentioning the product, or real-time pricing data. This contextual data adds depth to the product entity within the KG.
-
Reasoning with Context: KGs enable reasoning over connected entities, considering the relationships within the graph. Context stores can provide real-time updates or specific details that influence this reasoning process. Think of a recommendation system that leverages a KG to understand user preferences and product relationships.
Real-time stock data from a context store could influence the recommendation engine to suggest alternative products if a preferred item is out of stock.
-
Enriching Context with Knowledge: KGs can act as a source of structured context for the data within a context store.
For instance, a context store might hold user search queries related to a particular topic. A KG could link these queries to relevant entities and their relationships, providing a more comprehensive understanding of user intent behind the searches. These queries can be in the form of the on-site / in-app LLM powered chat interactions too.
Example: Customer Support (Knowledge Graphs and Context Stores)
Imagine a customer support scenario where a user has a question about a product.
- KG: Represents products, their features, warranties, and troubleshooting steps as interconnected entities.
- Context Store: Stores user purchase history, recent interactions with the support system, and real-time product availability data.
By working together:
- The KG can guide the support agent towards relevant troubleshooting steps based on the specific product and its features.
- The context store can inform the agent of the user’s past interactions and product ownership, allowing for a more personalized support experience.
- Real-time data from the context store could reveal if the product is experiencing a known issue, enabling the agent to address the user’s concern more efficiently.
Building a Context Store on GCP with BigTable and EKG
GCP provides powerful tools to build a robust and sophisticated Context Store. By leveraging BigTable for scalable storage and versioning, and EKG for structured context, you create a system that supports rich analytics and adaptive machine learning models.
Key Components:
-
BigTable: Serves as the foundation for storing diverse contextual data types. Its high-performance, scalability, and native versioning are ideal for capturing both real-time updates and historical context.
-
Cloud Enterprise Knowledge Graph (EKG): EKG introduces a structured context layer. It manages entities, their relationships, and rich metadata. This allows you to connect and represent complex relationships within your data.
-
Pub/Sub: A reliable messaging service for ingesting real-time updates from various context sources like user behavior tracking, IoT sensors, or external data streams.
-
Cloud Dataflow: This fully-managed service cleans, transforms, and enriches streamed context data from Pub/Sub. Dataflow can link context data to EKG entities or derive features for BigTable storage.
-
Cloud IAM: Enforce fine-grained access controls on all GCP resources (BigTable, EKG, Pub/Sub) for security and compliance.
Architecture
- Data Ingestion: Capture context updates from various sources using Pub/Sub.
- Real-time Processing: Employ Cloud Dataflow to process, enrich, and link context data with relevant EKG entities
- Storage:
- Utilize BigTable to store the primary context data, taking advantage of its versioning capabilities.
- Define and maintain entities and their relationships within Enterprise Knowledge Graph (EKG).
- Serving:
- Query BigTable directly for specific entities and historical versions of context data.
- Leverage EKG’s search capabilities to discover context based on related entities or complex relationships.
Example: Personalized Customer Support
Imagine you’re a customer facing an issue with a product. Wouldn’t it be ideal if the support system understood your purchase history, knew the product’s intricacies, and could access the latest troubleshooting information? Let’s dive into an example of how a BigTable and EKG-powered Context Store makes this possible:
- BigTable: Stores customer interaction histories (including timestamps), product purchase data, and real-time support ticket updates.
- EKG: Represents products, their features, known issues, and troubleshooting guides. EKG entities link to relevant support tickets, customer information, or product documentation.
- Support System: Leverages both BigTable’s historical context and EKG’s structured knowledge to provide:
- Personalized troubleshooting guidance based on the customer’s specific product configuration and support history.
- Access to related troubleshooting guides or known issues through EKG links.
Key Considerations:
- Schema Design: Optimize your BigTable schema and EKG entity modeling to match your data sources and the types of contextual queries you anticipate.
- Linking Context and Entities: Define processes (within Cloud Dataflow or Cloud Functions) for linking and updating the connections between your raw context data and its corresponding EKG entities.
- Access Patterns: Choose between BigTable’s API and EKG’s API based on whether your queries focus on retrieving full context histories or exploring relationships between context and entities.
Tailoring Data Pipelines: Understanding ELT-C Permutations
The classic Extract, Transform, Load (ETL) process has evolved to address the demands of modern data-driven organizations. By strategically incorporating the Contextualize (C) step at different points in the pipeline, we create several permutations. While in this post, We explored Contextualize(C) following an ETL step, the Context can be injected at any stage of the ETL process, and even multiple times.
Understanding these variations - ELT-C, ELT-C, EC-T, and even EL-C-T-C is key to designing a data pipeline that best aligns with your specific needs and data architecture. Let’s explore these permutations and their implications.
-
ETL-C (discussed in majority of this post above)
- ETL (Extract, Transform, Load): This is the traditional approach where data is:
- Extracted from source systems
- Transformed into a desired format and structure
- Loaded into a target data warehouse or lake
- C (Contextualize): After the data is cleaned and structured within the target system, an additional step enriches it by adding relevant context (metadata, external data, user interactions)
- ETL (Extract, Transform, Load): This is the traditional approach where data is:
-
ELT-C
- EL (Extract, Load): Emphasizes loading raw data into the target system as quickly as possible. Transformations and cleaning are deferred.
- T (Transform): Once in the target system (typically suitable for big data), transformations are applied, often leveraging the target system’s processing power.
- C (Contextualize): Similar to ETL-C, context is added as a final enrichment step.
-
EL-C-T
- EL (Extract, Load): Same as in ELT-C, raw data is prioritized for quick ingestion.
- C (Contextualize): Contextualization occurs immediately after loading, adding context while the data is still raw. This might involve linking external data or incorporating real-time insights.
- T (Transform): Finally, the now contextually enriched data undergoes transformations for cleaning, formatting, and structuring.
-
EL-C-T-C
- EL (Extract, Load): Identical initial step to the previous variations.
- C (Contextualize): Context is added after loading, as explained before.
- T (Transform): Transformations are applied.
- C (Contextualize): An additional contextualization layer is added after transformations. This might involve re-evaluating context based on the transformed data or deriving new contextual features.
When to Choose Which
The optimal permutation depends on factors like:
- Data Size and Velocity: If dealing with massive, rapidly changing data, ELT-C might prioritize rapid loading for analysis or model training.
- Need for Clean Data: Traditional
ETL-Cis still valuable when clean, structured data is a hard requirement for downstream systems. - Dynamic Context:
EL-C-TorEL-C-T-Care valuable when context is derived from the raw data itself or needs to be updated alongside transformations.
Do note that, these are not always strictly distinct. Modern data pipelines are often hybrid, employing elements of different patterns based on the specific data source or use case.
A EL-C-T-C Scenario
Scenario: Real-time Sentiment Analysis for Social Media
Challenge: Social media is a goldmine of raw customer sentiment, but extracting actionable insights quickly from its unstructured, ever-changing nature is complex.
How EL-C-T-C Helps:
-
Extract (E): A system continuously pulls raw social media data (posts, tweets, comments) from various platforms.
-
Load (L): The raw data is loaded directly into a scalable data lake for immediate accessibility.
-
Contextualize (C1): Initial contextualization is applied:
- Metadata: Timestamp, social platform, geo-location (if available)
- Basic Sentiment: Text analysis tools assign preliminary sentiment scores (positive, negative, neutral)
-
Transform (T):
- NLP: Natural Language Processing models extract key topics, product mentions, and finer-grained sentiment.
- Cleanup: Filters remove spam and irrelevant content.
-
Contextualize (C2): The transformed data is further enriched:
- Entity Linking: Identified brand and product mentions link to internal product Knowledge Graphs or external product databases.
- Trend Analysis: Data is cross-referenced with historical data for trend analysis. Are complaints about a particular feature increasing? Is positive sentiment surrounding a new competitor emerging?
Why EL-C-T-C Works Here:
- Speed: Raw data is ingested immediately, crucial for real-time analysis.
- Contextual Insights on Raw Data: Basic sentiment and metadata are added quickly, allowing for preliminary alerting on urgent issues.
- Evolving Context: The second contextualization layer refines sentiment, unlocks deeper insights (e.g., issues tied to specific features), and adds valuable trend context after transformations enhance the data.
Outcome
The business has a dashboard that not only tracks the real-time sentiment surrounding their brand and products, but can drill down on the drivers of those sentiments. This data empowers them to proactively address customer concerns, protect brand reputation, and make data-informed product and marketing decisions.
Is ELT-C the right choice for your data workflows? If you’re looking to fully unlock the potential of your data, I recommend giving this framework a closer look. Begin by identifying areas where integrating more context could substantially improve your analytics or machine learning models.
I’m eager to hear your perspective! Are you implementing ELT-C or similar methods in your organization? Please share your experiences and insights in the comments below.
]]>